Ulam Spiral

A prime is any number whose only factors are one and itself. These unique numbers do not follow the pattern of any other number we know about.

The search for some sort of pattern in prime numbers has been a quest since these unique numbers were discovered. Around 300 BC, Euclid challenged the belief that there could be a finite amount of prime numbers. His proof is one of the oldest theorems in math.

Throughout history, people have tried to find some sort of pattern among prime numbers. Can you find one? Fortunately for us, there is not a clear pattern for all the prime numbers. Why? Because the safety of our electronic transactions relies on the uniqueness of prime numbers. (See page IX for a more detailed explanation on that)

Stan Ulam (1909-1984) tried a new approach to looking at primes. He developed the spiral of numbers you see on the right. First he layed out all the whole numbers in a spiral. Second, he highlighted the prime numbers. Its that simple. There still doesn't seem to be any patterns using this method, although it is nice to look at.

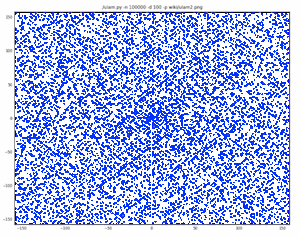
image credit: Charles Krohn, bitbucket.org/ctkrohn/ulam

image credit: Rob Rhinehart, robrhinehart.com/projects/ulam/docs.html

The above images show the Ulam Spiral when we zoom out even further. You can begin to see some diagonal lines taking shape in the picture on the left. On the right you can clearly make out these diagonal lines. Does it look like a pattern to you? Maybe it is, but the mathematicians haven't figured out the exact patterns just yet. Maybe we never will. Maybe you will.